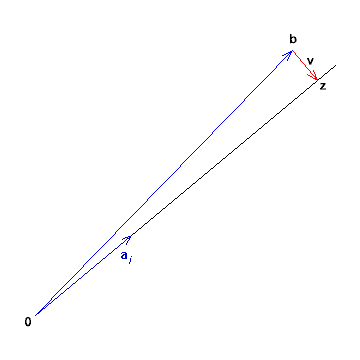
 Dieser Ansatz besitzt folgende geometrische Interpretation:
Dieser Ansatz besitzt folgende geometrische Interpretation:Gegeben seien m lineare Gleichungen für die
n gesuchten Größen x =
Es wird ferner vorausgesetzt, dass die n Spaltenvektoren
erfüllt wird3) und zugleich
gilt4) (Methode der kleinsten Quadrate).
 Dieser Ansatz besitzt folgende geometrische Interpretation:
Dieser Ansatz besitzt folgende geometrische Interpretation:
Gesucht wird ein Vektor z = A x =
und
gleichbedeutend (äquivalent).
Die Minimalität der Länge des Vektors v ist dann gegeben,
wenn die Vektoren z und v orthogonal sind, d. h. im rechten Winkel
zueinander stehen. Dies ist genau dann der Fall, wenn
schreiben lassen5), was mit der Gleichung
| AH A x = AH b |
gleichbedeutend ist. Dies ist ein lineares Gleichungssystem (n Gleichungen
mit n Unbekannten, die man als Normalgleichungen bezeichnet),
das unter der Voraussetzung der linearen Unabhängigkeit der Spaltenvektoren
1) Vektoren werden mit fetten, aufrechten Kleinbuchstaben, Matrizen mit fetten, aufrechten Großbuchstaben bezeichnet. (Zurück zum Bezug)
2) Der Vektor x ist ein Spaltenvektor; zwecks einer einfacheren Darstellung ist
er zunächst als Zeilenvektor angegeben, der Exponent T
besagt, dass der Vektor zu transponieren ist. Da das Transponieren eine Operation ist, die
sowohl auf Matrizen wie auch auf Vektoren (als einzeilige oder einspaltige Matrizen)
anwendbar ist, soll sie gleich für Matrizen erläutert werden. Ist A =
3) v bezeichnet den Vektor der Verbesserungen, die an die (gemessenen) Istwerte b anzubringen sind, damit sie die Sollwerte A x ergeben. (Zurück zum Bezug)
4) Wegen der einfacheren Darstellung mit Mitteln von HTML wird hier - soweit dem nichts entgegensteht - das Gauß'sche Summensymbol verwendet werden, was im Vermessungswesen gang und gäbe ist. Die Summe über i von 1 bis n der Größen vi wird so einfach in der Form [v] geschrieben, analog die Summe der Quadrate der reellen(!) Größen vi in der Form [vv], die sich gegenüber [v2] durchgesetzt hat. Hieraus leitet sich auch der Begriff Methode der kleinsten Quadrate ab. Für komplexe Zahlen ist [vv*] einzusetzen. (Zurück zum Bezug)
5) Zunächst ist festzuhalten, dass zu einer
Matrix A =
(ai,j)i=1(1)m,j=1(1)n die konjugiert komplexe Matrix durch A* =
(ai,j*)i=1(1)m,j=1(1)n definiert ist. Gleiches gilt für Vektoren.
Die Anwendung des Transponierens und der Bildung des konjugiert Komplexen auf eine
Matrix ist vertauschbar und wird als zusammengefasste Operation mit dem Exponenten
H kenntlich gemacht, also gilt
AH =
(AT)* =
(A*)T .
Der Buchstaben H bezieht sich im vorliegenden Zusammenhang auf den französischen
Mathematiker
C.
Hermite. Eine quadratische Matrix A heißt
hermitesch, wenn AH = A .
(Zurück zum Bezug)
| Zurück zur Hauptseite | Erstellt von Wolfgang Volk im September 2004 Zuletzt formal korrigiert am 4. September 2012 |